Heap Sort and Priority Queue
Heap Sort is a sorting technique using binary heap.
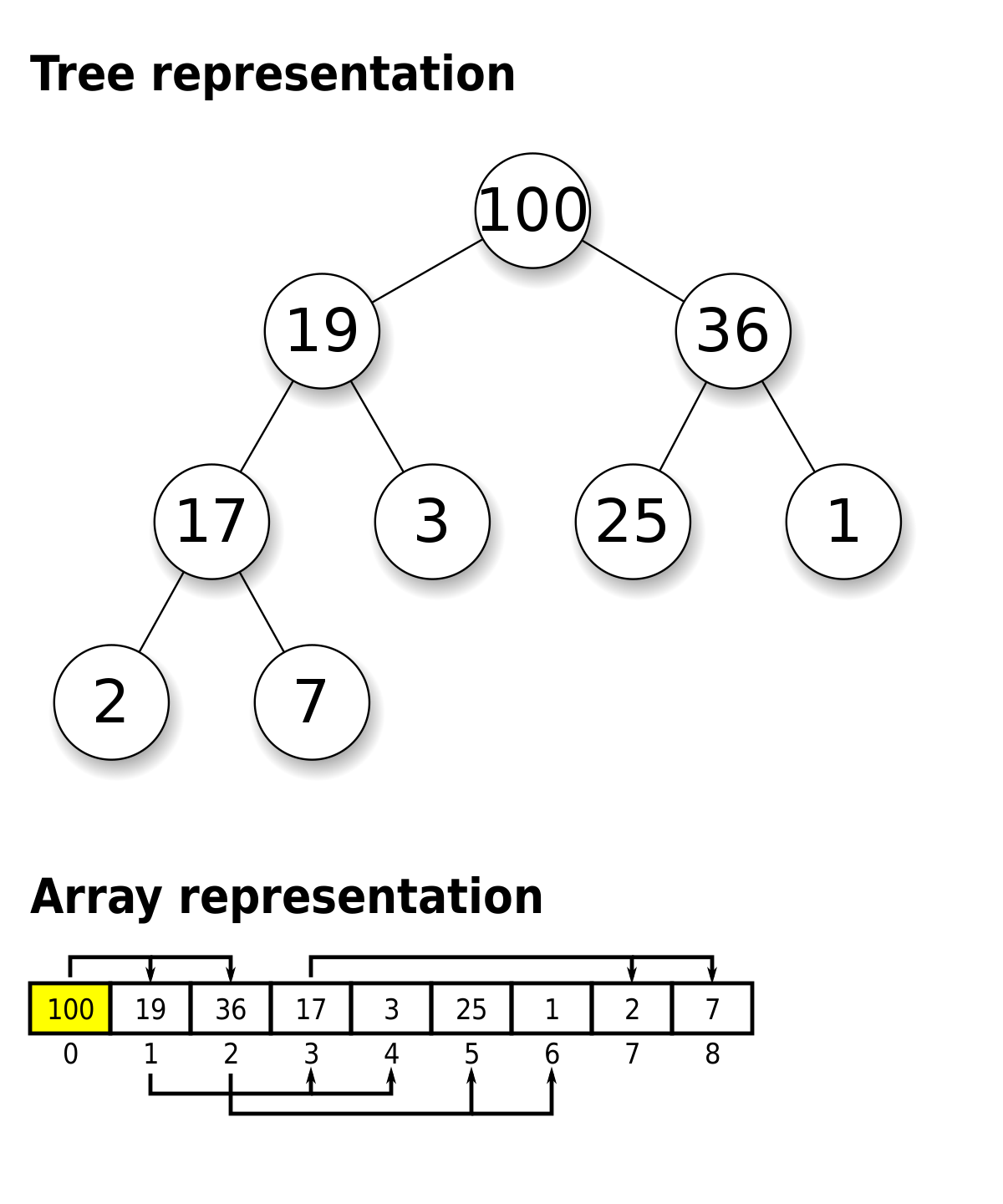
A Binary Heap is a binary tree where for a maximum binary heap is a heap with the parent node being smaller than the successive children nodes. A Binary Heap can be represented by an array, with a specific formula, it is very space-efficient.
# Python program for implementation of heap Sort
# To heapify subtree rooted at index i.
# n is size of heap
def heapify(arr, n, i):
largest = i # Initialize largest as root
l = 2 * i + 1 # left = 2*i + 1
r = 2 * i + 2 # right = 2*i + 2
# See if left child of root exists and is
# greater than root
if l < n and arr[largest] < arr[l]:
largest = l
# See if right child of root exists and is
# greater than root
if r < n and arr[largest] < arr[r]:
largest = r
# Change root, if needed
if largest != i:
arr[i], arr[largest] = arr[largest], arr[i] # swap
# Heapify the root.
heapify(arr, n, largest)
# The main function to sort an array of given size
def heapSort(arr):
n = len(arr)
# Build a maxheap.
for i in range(n//2 - 1, -1, -1):
heapify(arr, n, i)
# One by one extract elements
for i in range(n-1, 0, -1):
arr[i], arr[0] = arr[0], arr[i] # swap
heapify(arr, i, 0)
# Driver code
arr = [12, 11, 13, 5, 6, 7]
heapSort(arr)
n = len(arr)
print("Sorted array is")
for i in range(n):
print("%d" % arr[i]),
# This code is contributed by Mohit Kumra
Here is a sample code in Python: (From GeeksforGeeks)
Above is a sample code of Heap Sort from GeeksforGeeks.
A Priority Queue is a queue with a few tweaks in the limits and rules. Every element of the queue has a priority, if two elements have the same priority, they are dequeued by order, and of course, an element with higher priority is dequeued faster than an element with lower priority.
A useful example of Priority Queue is Dijkstra’s Shortest Path Algorithm.
Written on June 26, 2021