There are many types of sorting algorithms out there, such as the famous quick sort, bubble sort, insertion sort, and selection sort. Among these types, there is the merge sort, which I will be explaining right now.

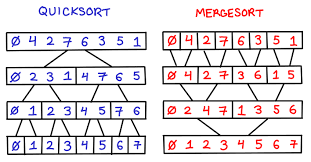
Merge Sort is a sorting algorithm, that uses divide and conquer to solve it. The steps are simple in Merge Sort.

1. The first thing we need to do is separate all the numbers in the array into their own separate arrays.
2. From there, we combine each of the arrays, sorting them during the process, until they are one big sorted array.

In coding terms, we would

1. Have a recursion function, constantly splitting the array in half, until the length is one.
2. Then, we combine the arrays that are length one, then constantly add each array and sort until the whole process is over.

Here is a sample code in Python:

def mergesort(ar):
    if len(ar) > 1:

        mid = len(ar)//2
        left, right = ar[:mid], ar[mid:]

        mergesort(left)
        mergesort(right)

        i, j, k = 0, 0, 0
        while i < len(left) and j < len(right):
            if left[i] < right[j]:
                ar[k] = left[i]
                i += 1
            else:
                ar[k] = (right[j])
                j += 1
            k += 1
        
        while i < len(left):
            ar[k] = (left[i])
            i += 1
            k += 1

        while j < len(right):
            ar[k] = (right[j])
            j += 1
            k += 1

ar = [4, 5, 7, 8, 9, 6]
mergesort(ar)
print(ar)

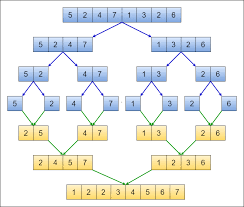
Now you may be wondering, why use Merge Sort? Merge Sort’s best, average, and worst case for running is all O(Nlog(N)).

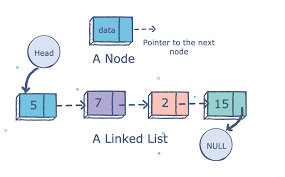
A primary example of using Merge Sort is when we sort linked lists; we can split all the nodes into individual parts, which then we would comebine and sort.

That’s it for Today’s Lesson. For more information, go to

https://www.geeksforgeeks.org/merge-sort/

Thank you!